深入解析比特币算术：从椭圆曲线到SHA-256算法

比特币作为一种革命性的数字货币，其背后有着复杂的算术原理。本文将深入探讨比特币算术的核心概念，包括椭圆曲线、有限域、SHA-256算法等，帮助读者更好地理解比特币的工作机制。

一、椭圆曲线与有限域

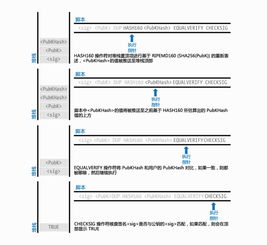
比特币的算术基础之一是椭圆曲线。椭圆曲线是一种特殊的数学曲线，其上的点可以进行加法运算。在比特币中，椭圆曲线被用来生成公钥和私钥。

椭圆曲线上的整数运算需要基于有限域。有限域是一种数学结构，其中的元素满足加法和乘法运算，并且这些运算的结果会进行模运算。在比特币中，有限域的阶通常为一个大质数，例如比特币使用的有限域阶为256。

例如，我们可以验证有限域的阶为103，从该字段中取出两个成员17和64，将它们组合为一个点坐标(17, 64)，该点在模103的曲线 y^2 = x^3 + 7 上。在有限域中，这个点的加法运算遵循特定的规则，确保运算结果仍然在有限域内。

二、SHA-256算法与比特币挖矿

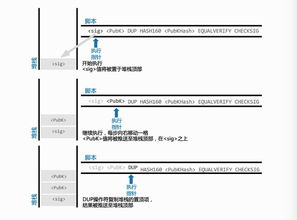
SHA-256是一种广泛使用的加密哈希算法，也是比特币挖矿过程中的核心算法。比特币挖矿的目标是找到满足特定条件的哈希值，这个过程被称为“挖矿”。

在比特币挖矿中，矿工需要解决一个数学难题，即找到一个随机数，使得该随机数与区块头中的某些信息组合后的SHA-256哈希值满足特定的难度要求。这个哈希值必须以特定的前导零开头，难度越高，前导零的数量越多。

SHA-256算法将输入数据（如区块头）转换为一个固定长度的哈希值。这个过程是不可逆的，即无法从哈希值反推出原始数据。这使得SHA-256成为比特币挖矿中确保安全性的关键。

三、比特币的共识机制

比特币的共识机制是确保网络中所有节点对账本达成一致的关键。比特币使用的工作量证明（Proof of Work，PoW）机制，要求矿工通过解决数学难题来验证交易并添加到区块链中。

在PoW机制中，矿工通过大量的计算来寻找满足特定条件的哈希值。这个过程不仅确保了交易的安全，还防止了双重支付攻击。当矿工找到正确的哈希值时，他们就会获得比特币奖励，并成为下一个区块的创建者。

然而，PoW机制也存在着能源消耗高、计算资源浪费等问题。因此，一些新的共识机制，如权益证明（Proof of Stake，PoS）和委托权益证明（Delegated Proof of Stake，DPoS），被提出以减少能源消耗和提高效率。

比特币的算术原理是构建其安全性和可靠性的基石。从椭圆曲线和有限域到SHA-256算法，再到共识机制，比特币的算术设计确保了其作为一个去中心化货币系统的可行性。通过理解这些算术概念，我们可以更好地欣赏比特币的复杂性和创新性。